Semana del 20 al 24 de abril de 2020
Deben copiar en el cuaderno lo que se muestra a continuación:
Problemas de tres conjuntos
Aquí se muestra la interpretación de las imágenes que contienen tres conjuntos la parte amarilla muestra lo que se explica mas abajo

Ahora resuelve los siguientes ejercicios:
Lo ideal es que se pueda realizar clases por ZOOM, Skipe o cualquiera otra aplicación que me permita explicar el tema.
Semana del 13 al 17 de Abril de 2020
Para esta semana trabajaremos con problemas de conjuntos para eso les invito a leer detenidamente el siguiente contenido y copiar un resumen en tu cuaderno de clases.
PROBLEMAS CON CONJUNTOS
Es posible usar los conceptos aprendidos para interpretar y resolver cierto tipo de problemas, aprende cómo hacerlo.
Observa la siguiente situación: en un salón de clases de niños y niñas, a les gusta solo el helado de fresa y a solo el helado de chocolate. Si a niños no les gusta el helado ni de fresa ni de chocolate: ¿a cuántos niños les gustan los dos helados?, ¿a cuántos niños les gusta en total el helado de fresa?, ¿a cuántos el de chocolate?
¡Mira la solución, es más sencilla de lo que crees! Primero representaremos la situación con diagramas de Venn: llamaremos al conjunto de los estudiantes a los que les gusta el helado de fresa y al de conjunto de niños que gustan del helado de chocolate.
Estos dos conjuntos deben estar contenidos en un conjunto universal, que es precisamente el salón de clase completo. Por lo tanto podemos representar toda la situación a través del siguiente diagrama.
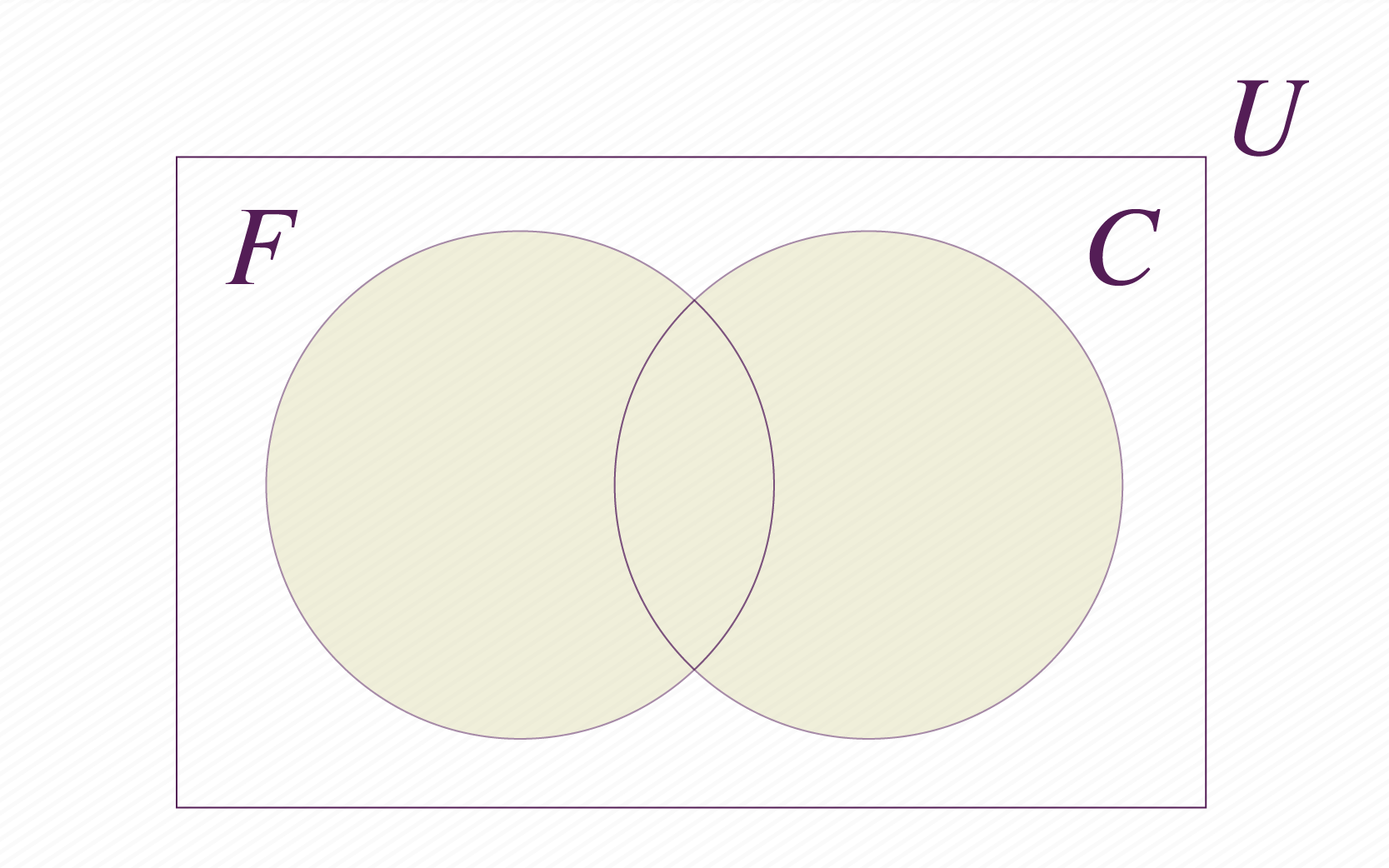
Las diferentes regiones del diagrama representan diferentes grupos de estudiantes. Por ejemplo, en la intersección de los conjuntos y , se representa la población de estudiantes que gustan de los dos helados, mientras que la región exterior a los conjuntos, representa la parte del curso que no gusta de ninguno. Podemos por lo tanto ubicar las cantidades de estudiantes en las zonas correspondientes:
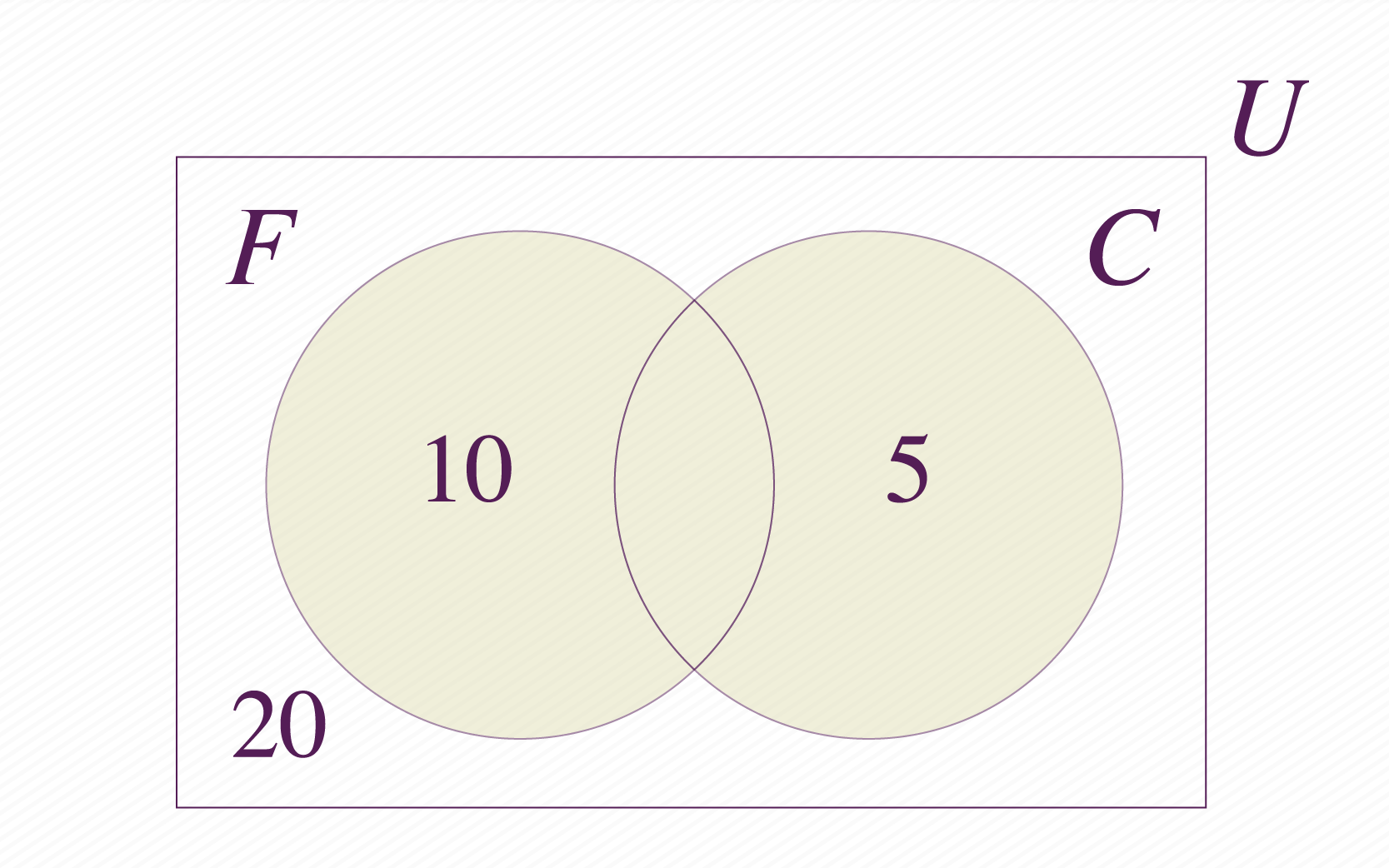
Observa que el y el quedaron ubicados en zonas que comprenden los estudiantes que gustan de solo de uno de los dos helados, por su parte el está ubicado por fuera de los dos conjuntos, representando los estudiantes que no gustan de estos sabores de helado, tal y como lo dice el enunciado del problema. Ahora bien, tenemos estudiantes que solo gustan del helado de fresa, solo el de chocolate y ninguno de los dos, lo que nos da un total de .
Como el curso completo se compone de estudiantes tenemos un faltante de . ¿A qué grupo pertenecen estos estudiantes?
Solo hay una opción: a la región que gusta de los dos helados, es decir la intersección de los conjuntos y .
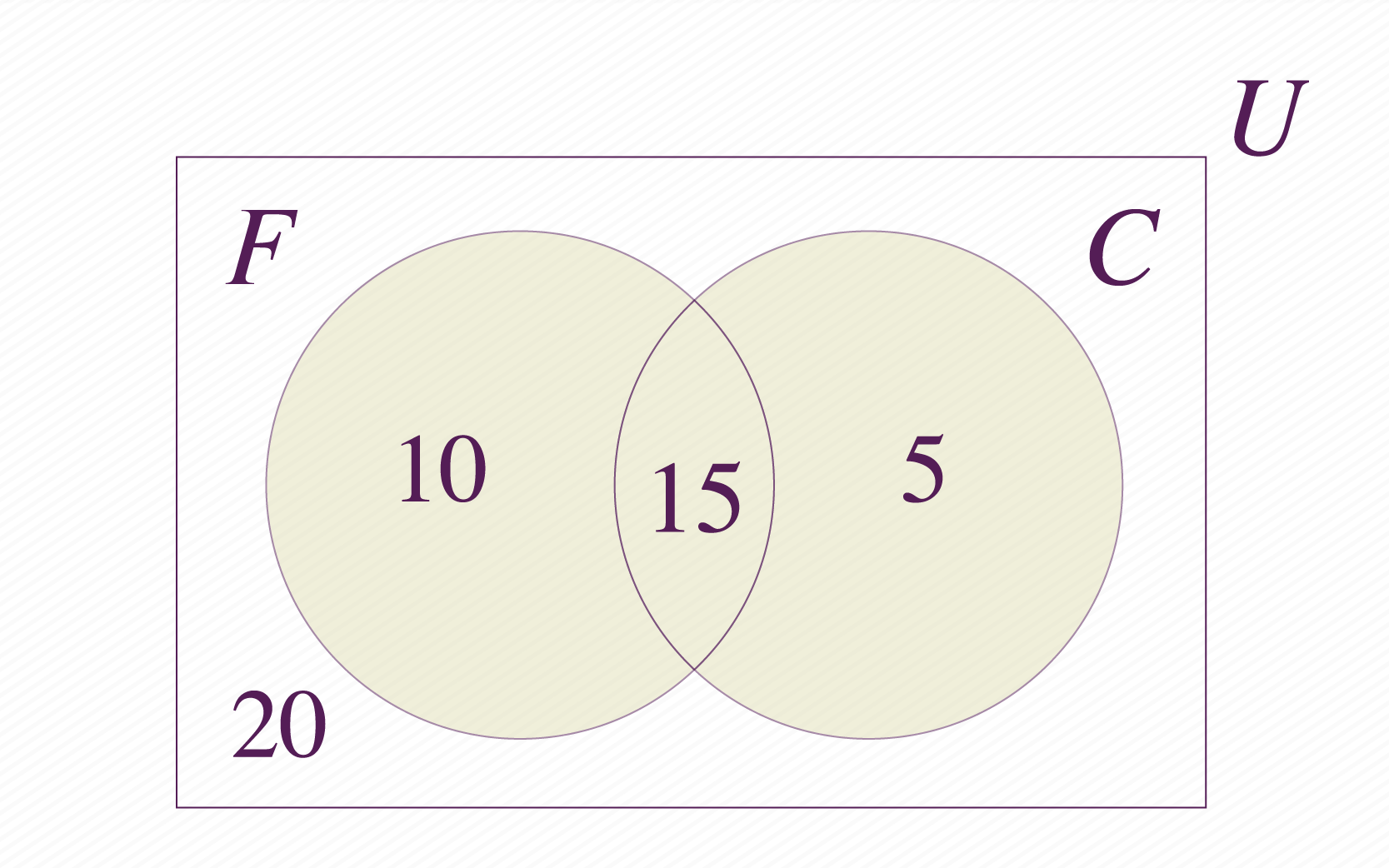
Podemos entonces responder todas las preguntas hechas inicialmente: a niños les gustan los dos helados, en total a les gusta el helado de fresa y a les gusta el helado de chocolate.
Resuelve en tu cuaderno los siguientes ejercicios.
- Cierto grupo de estudiantes rindió exámenes de CTA y Personal Social. Los resultados fueron los siguientes: 42 Aprobaron CTA, 16 aprobaron CTA y Personal Social, 28 aprobaron Personal Social y 6 no aprobaron examen alguno. ¿Cuántos estudiantes hay en el grupo?
- Se sabe que de 58 niños, 35 practican basquet, 28 voleibol y 18 los dos deportes. Determina cuántos niños no practican ninguno de estos deportes.
- Si de un grupo de 100 estudiantes, 50 aprobaron matemáticas, 38 Comunicación y 18 no aprobaron las dos áreas. Calcula cuántos aprobaron las dos áreas.
Si necesitas mas información accede al siguiente contenido
En este apartado encontrarás los enlaces para distintas actividades planificadas para la semana comprendida del 06 al 10 de Abril
Entre las actividades programadas se encuentra:
- Video explicativo de operaciones con conjuntos
- Ficha de ejercicios sobre operaciones con conjuntos
- Video explicativo de problema con dos conjuntos
- Ficha de ejercicios sobre problema con dos conjuntos
COMENCEMOS
Fecha de entrega de ficha y solución de la clase interactiva Miércoles 08 de Abril de 2020 Les adjunto el siguiente vídeo, lo que quiero que presten atención ahora son a las operaciones entres conjuntos:
- Unión
- Intersección
- Diferencia
- Diferencia simétrica
A en el link que se nuestra a continuación descargar ficha podrán descargar la ficha de ejercicios de esta ficha de ejercicios solo realizaran los ejercicios del 1 al 9 en su cuaderno y luego me envían la solución al correo: mates.iberoamericano@gmail.com.
Varias cosas a las que quiero que estén pendientes antes de ver el vídeo es a lo siguiente:
Cuando queremos expresar un conjunto lo podemos hacer de dos maneras :
- Por extensión
- Por comprensión
A ={ piña, papaya, mango, plátano}
Por Comprensión: Se indica la característica común de todos los elementos, es decir lo que se expresa en el conjunto es la cualidad común de los elementos. Por ejemplo: si quiero un conjunto de 4 elementos de frutas de color amarillo por comprensión estaría definido de la siguiente manera:
A ={x/x son cuatro frutas de color amarillo}
El cardinal del conjunto A viene expresado por n(A) que indica la cantidad de elementos no iguales del conjunto, como se muestra en los siguientes ejemplos:
Ejemplo 1:
Sea el conjunto A definido de la siguiente manera: A = { x/x son los meses del año}. Expresa el cardinal del conjunto A.
Vemos que el conjunto A esta expresado por comprensión (¿como se expresaría por extensión el conjunto A?) sabemos que los meses del año son 12 por lo tanto el cardinal del conjunto A seria 12, porque los mese del maño son todos distintos. Por lo tanto podemos expresar el cardinal del conjunto A, como sigue:
n(A) = 12
Ejemplo 2:
Sea el conjunto B definido de la siguiente manera: B = {1, 1, 2, 2, 3, 3, 4, 5, 4, 5}. Encuentra el cardinal de B [n(B) = ?]
Observamos que el conjunto se expresa por extensión y vemos que sus elementos no iguales son 1, 2, 3, 4 y 5 por lo tanto el cardinal del Conjunto B es 5 que se expresa n(B) = 5
Les anexo unos juegos que permitirán la evaluación por parte del estudiante si comprendió el tema estudiado.
Es importante señalar que esto a pesar de ser un juego también te va a permitir reconocer el avance en el tema estudiado, por lo tanto, se sugiere que se haga con la seriedad del caso y no solo como un juego trata de resolver en tu mente y luego haz lo que te pide la aplicación.
POR ULTIMO SOLO ME QUEDA DESEARLES ÉXITO EN ESTA ACTIVIDAD Y CUALQUIER DUDA O SUGERENCIA SOBRE LAS ACTIVIDADES PUEDEN HACERLAS POR MEDIO DEL CORREO mates.iberoamericano@gmail.com O EN LA CASILLA DE COMENTARIOS, GRACIAS DE ANTEMANO.



No hay comentarios:
Publicar un comentario